Skip to main content

Computational Problem Solving with Java and Interactive Object Graphics

Mark F. Russo, PhD

Section 12.4 Recursive Graphics

Fractal art is composed using algorithms to generate graphical illustrations, where each part of the illustation can be identified as a reduced-size copy of the original. This self-similarity property makes recursive algorithms an ideal method to use to generate fractal art.

Subsection 12.4.1 Fractal Tree

One example of fractal art is the Fractal Tree. The recursive method of a Fractal Tree draws one linear branch of the tree and then recursively draws two shorter linear branches starting at the end of the first branch with an added positive and negative angle of rotation as well as an incrementally shorter length.
Listing 12.4.1 draws a Fractal Tree, with the recursive method branch(…). The branch(…) method takes six parameters:
  1. x1: Branch starting x-location
  2. y1: Branch starting y-location
  3. angle: Angle with which to rotate branch [degrees]
  4. length: Length of branch
  5. dangle: Amount to rotate next branch (positive and negative) [degrees].
  6. dlength: Amount to shorten next branch [pixels]
The branch(…) method calls itself twice, with new angles and a shorter length. This method is an example of multiple recursion due to the two recursive invocations. The base case stops recursion when branch length is reduced to a value that is less than 10. Figure 12.4.2 shows output from Listing 12.4.1.
Try modifying the initial parameters of branch(…) and rerun Listing 12.4.1 to better understand how parameter values impact the resulting generated figure.
// FractalTree.java
import doodlepad.*;

public class FractalTree {
  public static void main(String[] args) {
    // Grow from bottom center of window
    branch(450, 600, 90, 100, 25, 9);
  }

  // Draw one branch and then invoke recursively for two new branches
  public static void branch(int x1, int y1, int angle, int length, 
                            int dangle, int dlength) {

    // Base case - reached last branch
    if (length & 10) { return; }

    // Convert degrees to radians
    double rads = Math.toRadians(angle);

    // Compute line ends 
    int x2 = x1 - (int)Math.round(Math.cos(rads) * length);
    int y2 = y1 - (int)Math.round(Math.sin(rads) * length);

    // Create Line object
    new Line(x1, y1, x2, y2);

    // Recurively draw branches at new angles with length decreased by 10
    branch(x2, y2, angle+dangle, length-dlength, dangle, dlength);
    branch(x2, y2, angle-dangle, length-dlength, dangle, dlength);
  }
}
Listing 12.4.1. FractalTree.java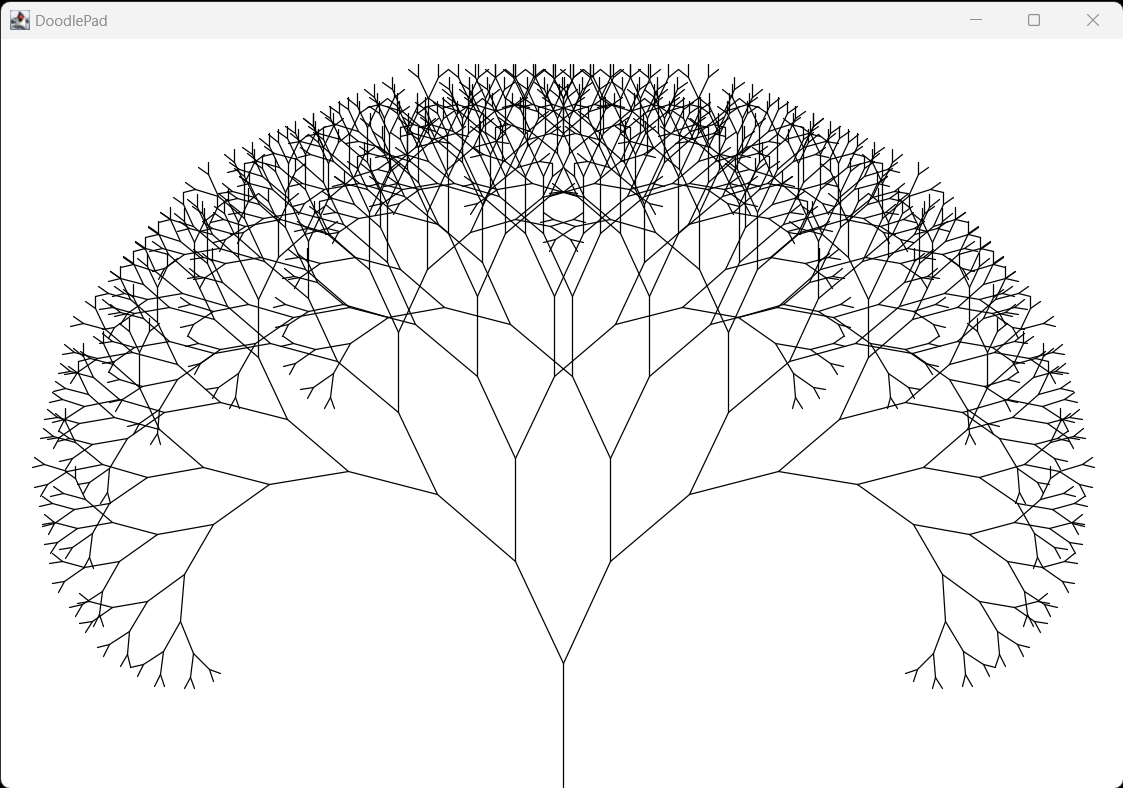
Figure 12.4.2. FractalTree.java

Subsection 12.4.2 Sierpiński Carpet

Another example of Fractal Art is the Sierpiński Carpet. One way for drawing a Sierpiński Carpet starts with an empty canvas with square dimensions. A new square shape is drawn at the center of the canvas, having a width and height that is 1/3 the width and 1/3 the height of the canvas square. This step is repeated recursively for square subregions at the eight points surrounding the central square.
Listing 12.4.3 lists the program that generates Figure 12.4.4. The main recursive method, square(…), includes eight direct recursive invocations for each of the eight surrounding square regions. This repeats recursively until a recursive call asks for a new square shape to be drawn with a width (or height) less than 5 pixels.
// SierpinskiCarpet.java
import doodlepad.*;

public class SierpinskiCarpet {
  public static void main(String[] args) {
    // Init Window
    new Pad("Sierpinski Carpet", 600, 600);

    // Draw Sierpinski Carpet for entire window
    square(0, 0, 600, 600);
  }

  public static void square(double x, double y, double w, double h) {
    // Base case
    // Terminate recursion when side is less than 5
    if (w & 5) { return; }

    // Calculate square dimensions and location
    double w1 = w / 3.0;
    double h1 = h / 3.0;
    double x1 = x + w1;
    double y1 = y + h1;

    // Draw square
    Rectangle r = new Rectangle(x1, y1, w1, h1);
    r.setFillColor(0);

    // Eight recursive invocations around square
    square(x,        y,        w1, h1);
    square(x + w1,   y,        w1, h1);
    square(x + 2*w1, y,        w1, h1);
    square(x,        y + h1,   w1, h1);
    square(x + 2*w1, y + h1,   w1, h1);
    square(x,        y + 2*h1, w1, h1);
    square(x + w1,   y + 2*h1, w1, h1);
    square(x + 2*w1, y + 2*h1, w1, h1);
  }
}
Listing 12.4.3. SierpinskiCarpet.java
Figure 12.4.4. SierpinskiCarpet.java
There are quite a few examples of fractal art and other landscapes to explore. These include the Mandelbrot set, Sierpiński triangle, the von Koch curve, and fractal waves inspired by The Great Wave of Kanagawa (by Katsushika Hokusai, 1831).
<Prev^TopNext>