Section 13.1 Algorithm Complexity
As we investigate various algorithms, we will benefit from having one or more metrics with which to compare them. We want these metrics to measure the utilization of scarce resources because this is what limits performance. The two key metrics that we consider are how the utilization of time and the utilization of space (memory) grows as the size of the problem being solved grows. The size of a problem is characterized by the parameter \(N\text{,}\) which measures the number of elements to be processed in a problem. For example, \(N\) might be the number of items to be searched or the number of items to be sorted. We refer to these two metrics as time complexity and space complexity, the derivation of which is called complexity analysis.
Algorithm complexity is often reported as one or more of three metrics: worst-case complexity, best-case complexity, and average-case complexity. Worst-case complexity measures the theoretical upper bound on resource utilization as a function of the problem size (\(N\)). Similarly, best-case complexity is the theoretical lower bound, and average-case complexity is the theoretical mean performance as a function of problem size (\(N\)). Each is written with its own Greek letter notation:
| Complexity | Notation | Pronunciation |
|---|---|---|
| worst-case | \(O(…)\) | Big O |
| best-case | \(\Omega(…)\) | Omega |
| average-case | \(\Theta(…)\) | Theta |
Whenever the modifier worst, best, or average, is left out of a complexity analysis discussion, we are usually talking about worst-case complexity. It is worst-case complexity that tells us the theoretical maximum amount of resources that we may need to solve a given problem.
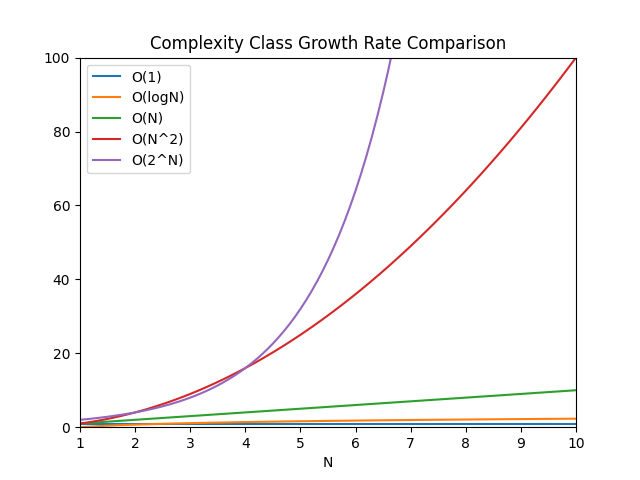
Common complexity classes are listed in Table 13.1.2. The rows of the table are ordered based on decreasing performance. In other words, A \(O(LogN)\) (logarithmic complexity) algorithm performs better than a \(O(N)\) (linear complexity) algorithm, which performs better than a \(O(N^2)\) (polynomial complexity) algorithm. Knowing this order will help you compare algorithms at a glance.
| Notation | Name | Description |
|---|---|---|
| \(O(1)\) | Constant complexity | Complexity does not grow with size of problem \(N\) |
| \(O(logN)\) | Logarithmic complexity | Complexity grows with rate dominated by a term in \(log(N)\) |
| \(O(N)\) | Linear complexity | Complexity grows with a rate proportional to \(N\) |
| \(O(N logN)\) | Linearithmic complexity | Complexity grows with rate dominated by \(N log(N)\) term |
| \(O(N^2)\text{,}\) \(O(N^3)\text{,}\) … | Polynomial complexity | Complexity grows with rate dominated by a power of \(N\) |
| \(O(2^N)\text{,}\) \(O(3^N)\text{,}\) … | Exponential complexity | Complexity grows with rate dominated by a term with \(N\) in the exponent |
Time Complexity measures the amount of time an algorithm takes to execute as a function of the input size (\(N\)).
Space Complexity measures the amount of memory an algorithm uses to solve a problem as a function of the input size (\(N\)).
Space complexity considers both the memory required for the algorithm’s code (instruction space) and the memory required to store data (data space). Algorithms that use additional data structures, like arrays or collections, may have higher space complexity due to the memory needed to store these structures.
It’s important to add that the complexities mentioned are theoretical and might not perfectly represent the real-world behavior of an algorithm. Constants and lower-order terms are often omitted in complexity notation, focusing on the growth rate (shape) of the function as the input size grows. Additionally, the actual performance of an algorithm can be influenced by factors such as hardware, compiler optimizations, and the nature of algorithm input.
When comparing algorithms, it’s common to prioritize those with lower time and space complexities, as they generally perform better for larger inputs. However, there can be trade-offs between time and space complexity. Some algorithms might have lower time complexity but higher space complexity, and vice versa. The choice of algorithm often depends on the specific requirements of the problem and the available resources.
As we begin to explore our algorithms, we’ll characterize them in terms of complexity. This will give us a way to compare them to each in terms of theoretical performance.
