Section 7.6 Polygons
A Polygon is a closed multi-sided shape made up of three or more straight lines connected end-to-end with the end of one line attached to the beginning of the next. Polygons are created by specifying an ordered sequence of vertices that define the endpoints of all polygon edges. Think of a triangle, square, pentagon, hexagon, etc. In DoodlePad the
Polygon class is used to create any polygon that you can imagine. A polygon may be convex or even concave at certain points. It is entirely up to you to choose the coordinates of the vertices.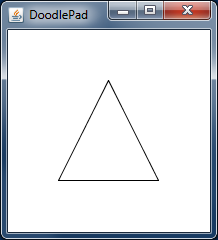
The Polygon class defines several constructors for you to use to create new Polygon shapes. One category takes two arrays: one holding all x-coordinates and a second holding corresponding y-coordinates. These arrays may be of type
double[] or int[].The following example program creates a Polygon object in the shape of a triangle (three vertices). Figure 7.6.1 is the output generated by this program.
// PolygonDemo1.java
import doodlepad.*;
public class PolygonDemo1 {
public static void main(String[] args) {
// Create and initialize two double[] arrays
double[] Xs = new double[] { 50.0, 100.0, 150.0};
double[] Ys = new double[] {150.0, 50.0, 150.0};
// Pass arrays to Polygon constructor
Polygon p1 = new Polygon(Xs, Ys);
}
}
Let’s write a method that creates regular star-shaped polygons with an arbitrary number of points greater than or equal to 2. Note that the number of vertices in a star-shaped polygon is twice the number of its points. Half are used for the inner concave vertices and the other half for the outer convex vertices (points of the star).
One way to think about how to make a star-shaped polygon is to imagine two concentric circles. The star’s concave vertices fall on the inner circle and its convex vertices on the outer circle. To collect vertex coordinates, we rotate around the complete \(2\pi\) radians of the circle with an incremental angle of \(\pi/N\text{,}\) where \(N\) is the number of the star’s points. As we rotate, we alternate the selection of vertices between the inner circle and the outer circle, at the current total angle. After one complete rotation, the sequence of vertex coordinates form the star-shaped polygon.
The
makeStar(…) method in Listing 7.6.3 builds and returns a star-shaped polygon, programmatically, using the technique described above. The method takes five parameters:npoints, the number of points in the starinrad, the radius of the inner circleoutrad, the radius of the outer circlexoffset, the offset of the star location in the x-directionyoffset, the offset of the star location in the y-direction
// MakeStar.java
import doodlepad.*;
// Demonstrate the makeStar(...) method
public class MakeStar {
public static void main(String[] args) {
Polygon star1 = makeStar(5, 100, 40, 150, 150); // 5-point star
Polygon star2 = makeStar(50, 100, 40, 150, 350);// 50-point star
star1.setFillColor(255, 255, 0); // Fill
star2.setFillColor(255, 0, 0);
}
// Create an return a Polygon object in shape of a star with npoints
// Parameters: num points, inner radius, outer radius, x- and y- offset
public static Polygon makeStar( int npoints,
double outrad, double inrad,
double xoffset, double yoffset) {
double[] Xs = new double[2*npoints]; // Vertex coordinates
double[] Ys = new double[2*npoints];
double dangle = (Math.PI / npoints); // Angle between vertices
double angle = -0.5*Math.PI; // One point on top
// Compute vertex coordinates. Two per iteration.
for (int i = 0; i<2*npoints; i += 2) {
// Outer vertex (convex/star point)
Xs[i] = xoffset + outrad * Math.cos(angle);
Ys[i] = yoffset + outrad * Math.sin(angle);
angle += dangle;
// Inner vertex (concave point)
Xs[i+1] = xoffset + inrad * Math.cos(angle);
Ys[i+1] = yoffset + inrad * Math.sin(angle);
angle += dangle;
}
// Instantiate and return a new Star-shaped Polygon
return new Polygon(Xs, Ys);
}
}
javac -cp doodlepad.jar MakeStar.java java -cp .;doodlepad.jar MakeStar
Figure 7.6.4 shows the output of running the program in Listing 7.6.3. The red 50-point star is composed of 100 vertices. Building this polygon from scratch would be far too tedious to do by hand. Fortunately, with a bit of reasoning, a couple arrays, and iteration, we can accomplish this relatively easily.

MakeStar.java